• 11.7 移动窗口函数
    • 指数加权函数
    • 二元移动窗口函数
    • 用户定义的移动窗口函数

    11.7 移动窗口函数

    在移动窗口（可以带有指数衰减权数）上计算的各种统计函数也是一类常见于时间序列的数组变换。这样可以圆滑噪音数据或断裂数据。我将它们称为移动窗口函数（moving window function），其中还包括那些窗口不定长的函数（如指数加权移动平均）。跟其他统计函数一样，移动窗口函数也会自动排除缺失值。

    开始之前，我们加载一些时间序列数据，将其重采样为工作日频率：

    1. In [235]: close_px_all = pd.read_csv('examples/stock_px_2.csv',
    2.    .....:                            parse_dates=True, index_col=0)
    4. In [236]: close_px = close_px_all[['AAPL', 'MSFT', 'XOM']]
    6. In [237]: close_px = close_px.resample('B').ffill()

    现在引入rolling运算符，它与resample和groupby很像。可以在TimeSeries或DataFrame以及一个window（表示期数，见图11-4）上调用它：

    1. In [238]: close_px.AAPL.plot()
    2. Out[238]: <matplotlib.axes._subplots.AxesSubplot at 0x7f2f2570cf98>
    4. In [239]: close_px.AAPL.rolling(250).mean().plot()

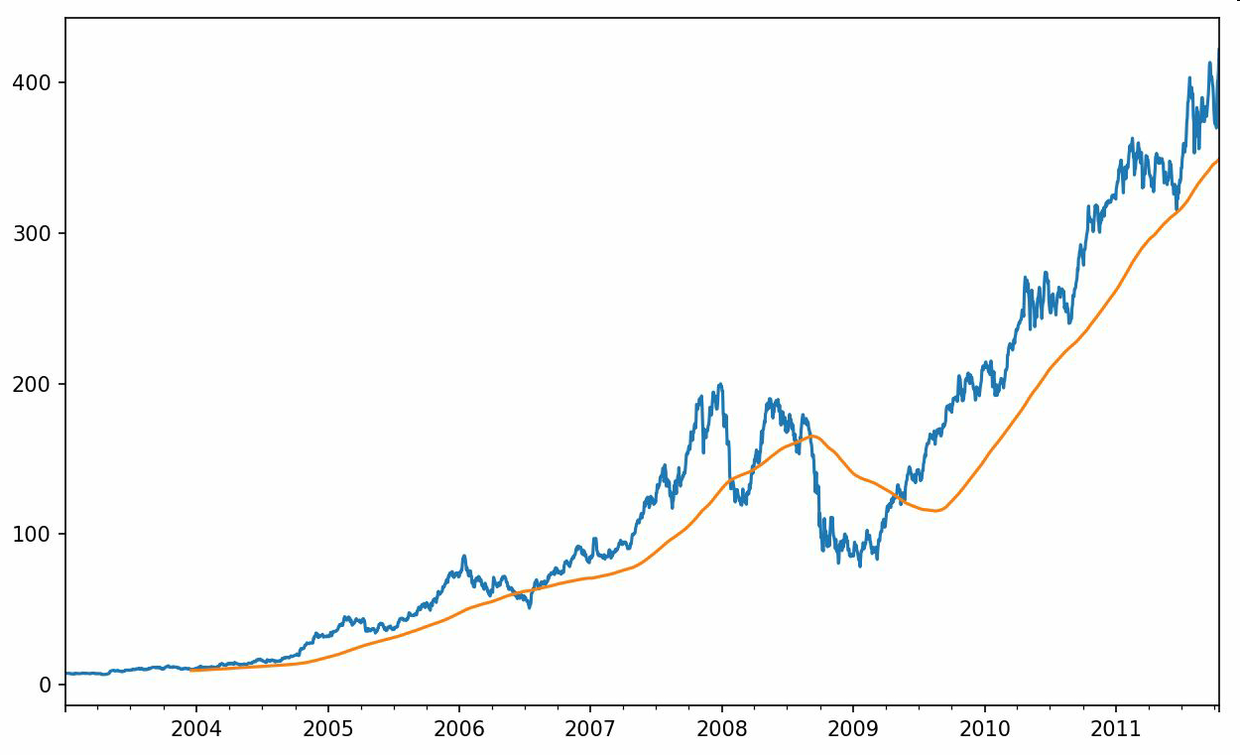
    图11-4 苹果公司股价的250日均线

    表达式rolling(250)与groupby很像，但不是对其进行分组，而是创建一个按照250天分组的滑动窗口对象。然后，我们就得到了苹果公司股价的250天的移动窗口。

    默认情况下，rolling函数需要窗口中所有的值为非NA值。可以修改该行为以解决缺失数据的问题。其实，在时间序列开始处尚不足窗口期的那些数据就是个特例（见图11-5）：

    1. In [241]: appl_std250 = close_px.AAPL.rolling(250, min_periods=10).std()
    3. In [242]: appl_std250[5:12]
    4. Out[242]: 
    5. 2003-01-09         NaN
    6. 2003-01-10         NaN
    7. 2003-01-13         NaN
    8. 2003-01-14         NaN
    9. 2003-01-15    0.077496
    10. 2003-01-16    0.074760
    11. 2003-01-17    0.112368
    12. Freq: B, Name: AAPL, dtype: float64
    14. In [243]: appl_std250.plot()

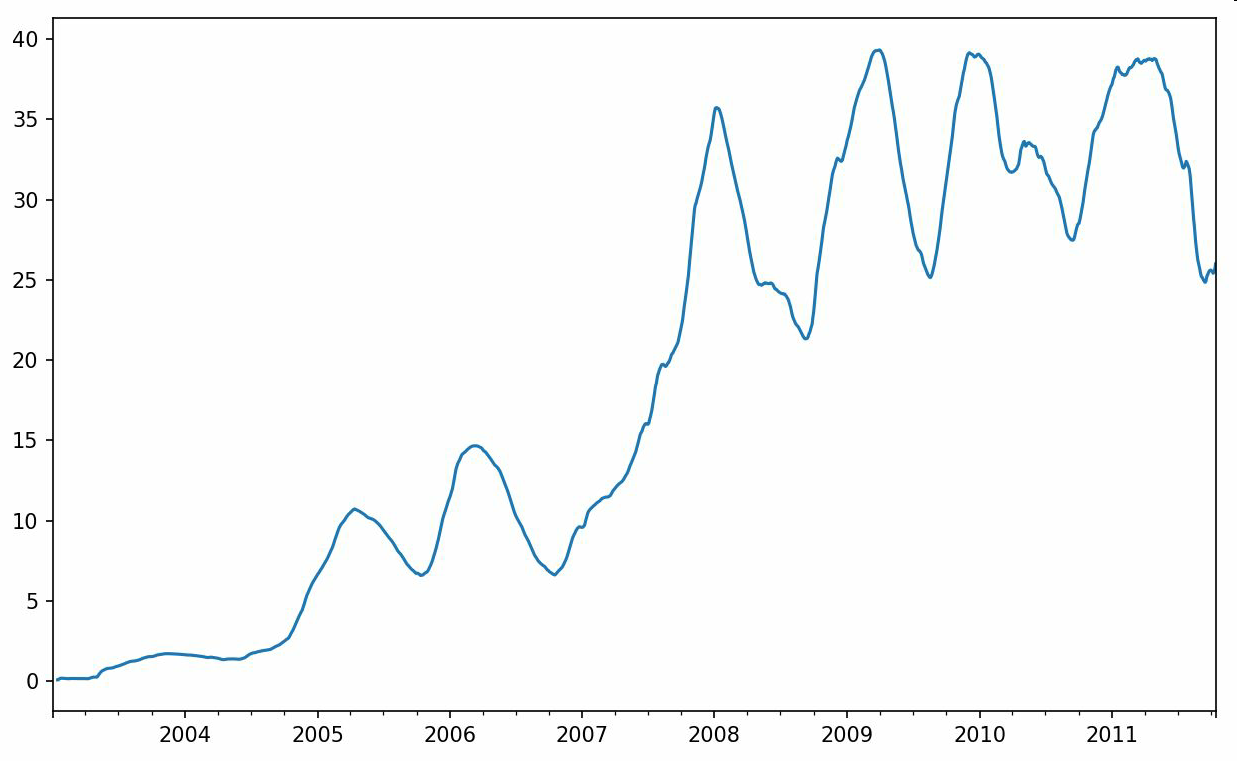
    图11-5 苹果公司250日每日回报标准差

    要计算扩展窗口平均（expanding window mean），可以使用expanding而不是rolling。“扩展”意味着，从时间序列的起始处开始窗口，增加窗口直到它超过所有的序列。apple_std250时间序列的扩展窗口平均如下所示：

    1. In [244]: expanding_mean = appl_std250.expanding().mean()

    对DataFrame调用rolling_mean（以及与之类似的函数）会将转换应用到所有的列上（见图11-6）：

    1. In [246]: close_px.rolling(60).mean().plot(logy=True)

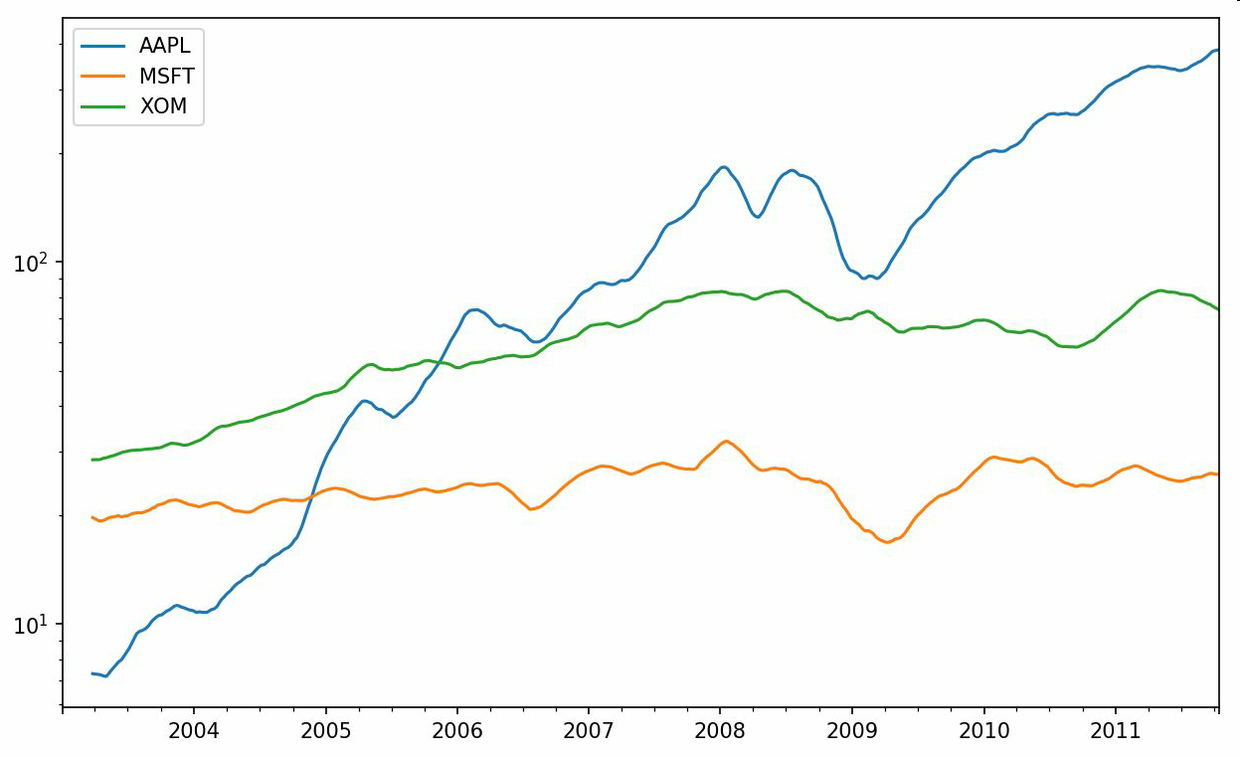
    图11-6 各股价60日均线（对数Y轴）

    rolling函数也可以接受一个指定固定大小时间补偿字符串，而不是一组时期。这样可以方便处理不规律的时间序列。这些字符串也可以传递给resample。例如，我们可以计算20天的滚动均值，如下所示：

    1. In [247]: close_px.rolling('20D').mean()
    2. Out[247]:
    3.                   AAPL       MSFT        XOM
    4. 2003-01-02    7.400000  21.110000  29.220000
    5. 2003-01-03    7.425000  21.125000  29.230000
    6. 2003-01-06    7.433333  21.256667  29.473333
    7. 2003-01-07    7.432500  21.425000  29.342500
    8. 2003-01-08    7.402000  21.402000  29.240000
    9. 2003-01-09    7.391667  21.490000  29.273333
    10. 2003-01-10    7.387143  21.558571  29.238571
    11. 2003-01-13    7.378750  21.633750  29.197500
    12. 2003-01-14    7.370000  21.717778  29.194444
    13. 2003-01-15    7.355000  21.757000  29.152000
    14. ...                ...        ...        ...
    15. 2011-10-03  398.002143  25.890714  72.413571
    16. 2011-10-04  396.802143  25.807857  72.427143
    17. 2011-10-05  395.751429  25.729286  72.422857
    18. 2011-10-06  394.099286  25.673571  72.375714
    19. 2011-10-07  392.479333  25.712000  72.454667
    20. 2011-10-10  389.351429  25.602143  72.527857
    21. 2011-10-11  388.505000  25.674286  72.835000
    22. 2011-10-12  388.531429  25.810000  73.400714
    23. 2011-10-13  388.826429  25.961429  73.905000
    24. 2011-10-14  391.038000  26.048667  74.185333
    25. [2292 rows x 3 columns]

    指数加权函数

    另一种使用固定大小窗口及相等权数观测值的办法是，定义一个衰减因子（decay factor）常量，以便使近期的观测值拥有更大的权数。衰减因子的定义方式有很多，比较流行的是使用时间间隔（span），它可以使结果兼容于窗口大小等于时间间隔的简单移动窗口（simple moving window）函数。

    由于指数加权统计会赋予近期的观测值更大的权数，因此相对于等权统计，它能“适应”更快的变化。

    除了rolling和expanding，pandas还有ewm运算符。下面这个例子对比了苹果公司股价的30日移动平均和span=30的指数加权移动平均（如图11-7所示）：

    1. In [249]: aapl_px = close_px.AAPL['2006':'2007']
    3. In [250]: ma60 = aapl_px.rolling(30, min_periods=20).mean()
    5. In [251]: ewma60 = aapl_px.ewm(span=30).mean()
    7. In [252]: ma60.plot(style='k--', label='Simple MA')
    8. Out[252]: <matplotlib.axes._subplots.AxesSubplot at 0x7f2f252161d0>
    10. In [253]: ewma60.plot(style='k-', label='EW MA')
    11. Out[253]: <matplotlib.axes._subplots.AxesSubplot at 0x7f2f252161d0>
    13. In [254]: plt.legend()

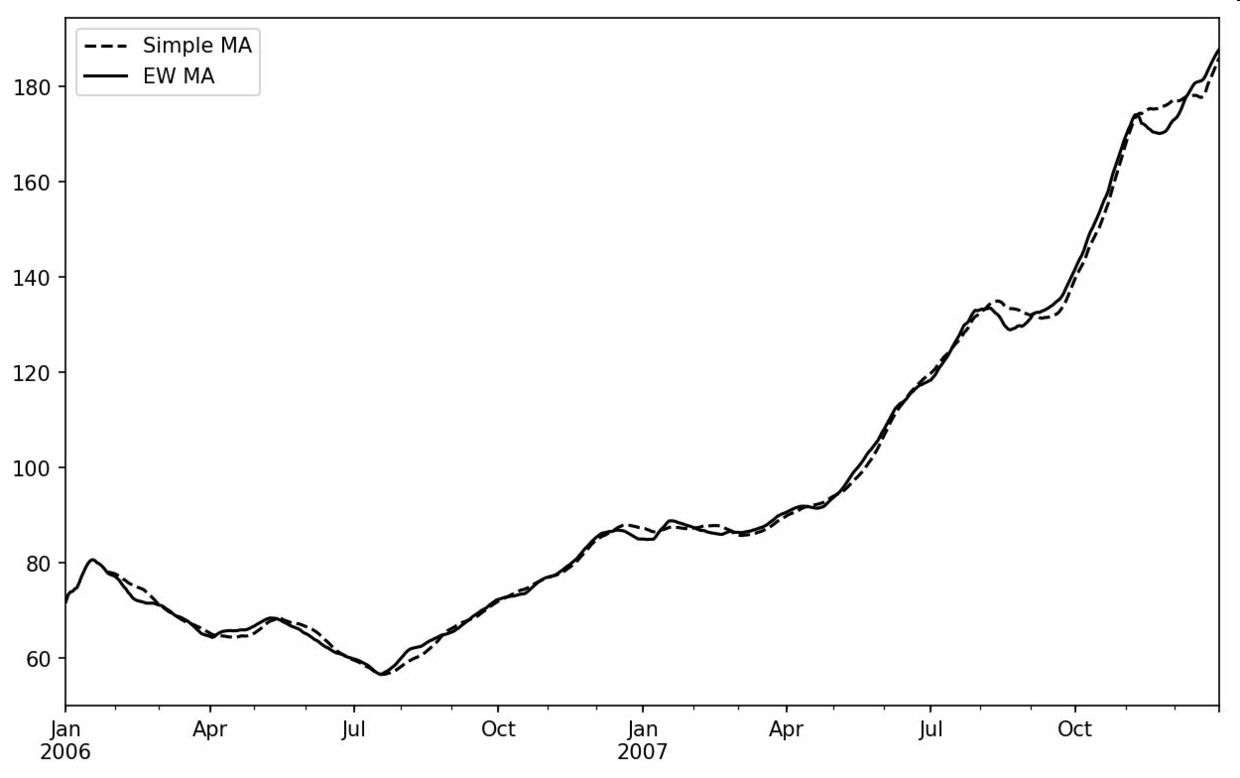
    图11-7 简单移动平均与指数加权移动平均

    二元移动窗口函数

    有些统计运算（如相关系数和协方差）需要在两个时间序列上执行。例如，金融分析师常常对某只股票对某个参考指数（如标准普尔500指数）的相关系数感兴趣。要进行说明，我们先计算我们感兴趣的时间序列的百分数变化：

    1. In [256]: spx_px = close_px_all['SPX']
    3. In [257]: spx_rets = spx_px.pct_change()
    5. In [258]: returns = close_px.pct_change()

    调用rolling之后，corr聚合函数开始计算与spx_rets滚动相关系数（结果见图11-8）：

    1. In [259]: corr = returns.AAPL.rolling(125, min_periods=100).corr(spx_rets)
    3. In [260]: corr.plot()

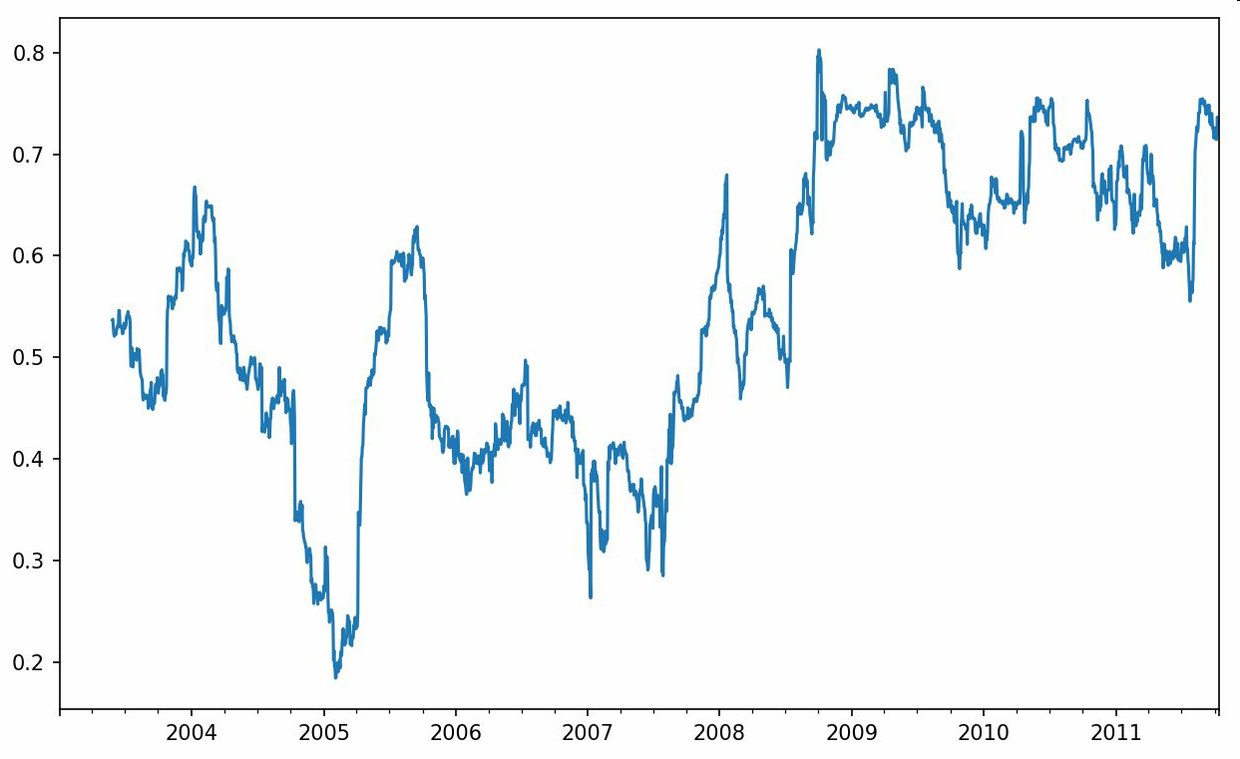
    图11-8 AAPL 6个月的回报与标准普尔500指数的相关系数

    假设你想要一次性计算多只股票与标准普尔500指数的相关系数。虽然编写一个循环并新建一个DataFrame不是什么难事，但比较啰嗦。其实，只需传入一个TimeSeries和一个DataFrame，rolling_corr就会自动计算TimeSeries（本例中就是spx_rets）与DataFrame各列的相关系数。结果如图11-9所示：

    1. In [262]: corr = returns.rolling(125, min_periods=100).corr(spx_rets)
    3. In [263]: corr.plot()

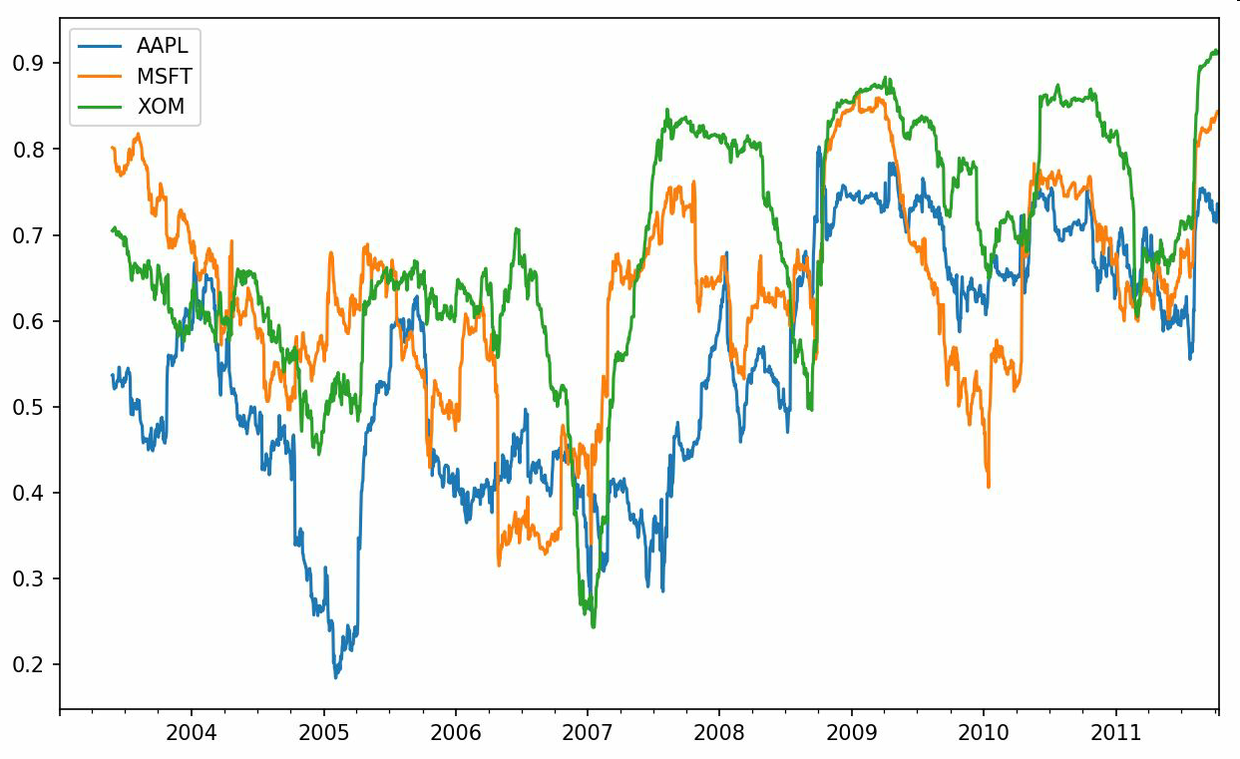
    图11-9 3只股票6个月的回报与标准普尔500指数的相关系数

    用户定义的移动窗口函数

    rolling_apply函数使你能够在移动窗口上应用自己设计的数组函数。唯一要求的就是：该函数要能从数组的各个片段中产生单个值（即约简）。比如说，当我们用rolling(…).quantile(q)计算样本分位数时，可能对样本中特定值的百分等级感兴趣。scipy.stats.percentileofscore函数就能达到这个目的（结果见图11-10）：

    1. In [265]: from scipy.stats import percentileofscore
    3. In [266]: score_at_2percent = lambda x: percentileofscore(x, 0.02)
    5. In [267]: result = returns.AAPL.rolling(250).apply(score_at_2percent)
    7. In [268]: result.plot()

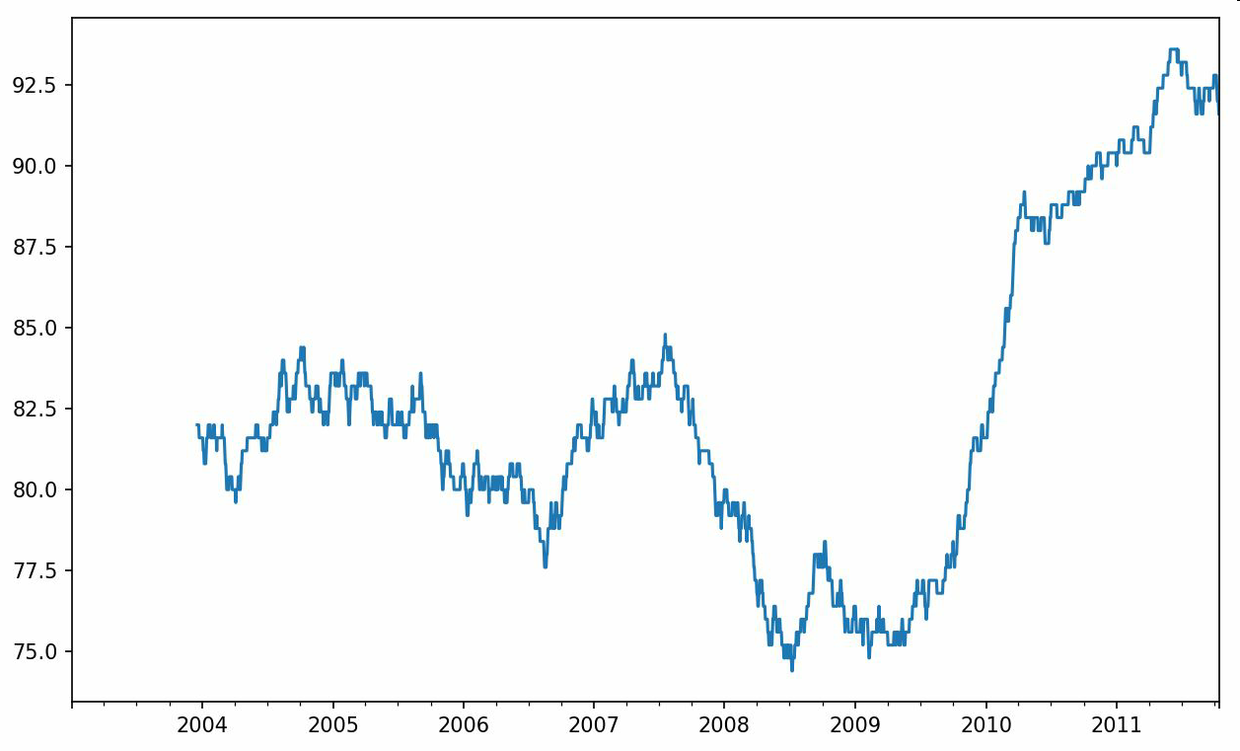
    图11-10 AAPL 2%回报率的百分等级（一年窗口期）

    如果你没安装SciPy，可以使用conda或pip安装。